|
阅读:4497回复:1
揭秘永远赢钱的马丁格尔策略
所谓「马丁格尔(Martingale)策略」是在某个赌盘里,当每次「输钱」时就以 2 的倍数再增加赌金,直到赢钱为止。
假设在一个公平赌大小的赌盘,开大与开小都是 50% 的概率,所以在任何一个时间点上,我们赢一次的概率是 50%,连赢两次的概率是 25%,连赢三次的概率 12.5%,连赢四次的概率 6.25%,以此类推。因此,以概率来算,如果连赢四次的概率 6.25%,也就是说连输四次的概率一样也只有6.25%。 假设我们有 63 元,按照马丁格尔策略理论来算的话,63 元的连续亏损如下:
所以只能容许「连续亏损」6 次,概率是:
假如我们玩「押大小」,当我们与庄家对赌 73 次,在某个点「连续亏损 6 次」的概率是 41.7%,算法为(证明可以跳过不看,不影响阅读):
同理:
所以马丁格尔策略风险相当高,别别别,客官先别走,其实今天介绍的不是马丁格尔策略,而是「反马丁格尔策略(Anti-Martingale)」。 「反马丁格尔(Anti-Martingale)策略」,是在某个赌盘里,当每次赌金「赢钱」时就以 2 的倍数再增加赌金,若一直赢,就再加倍赌注。(直到某个目标次数,再重新开始) 再假设我们有 63 元,第一次我们都从 1 元开始押注,我们选择使用「反马丁格尔策略」,每赢一次赌注都以 2 的倍数递增。也就是 1,2,4,8,16,32 一直递增的方式来押注。因此,当我们连押四次都输钱的概率是 6.25%(前面算过),我们会输掉 4 元。同样,同样的概率下,连赢四次,那我们将会赢得:
所以在「同一个概率点」上,我们会「输掉 4 元」或「赢得 15 元」,我们看看其他概率点;
是不是有点迷糊,我们一步一步看: 假如目标是连赢四次才会从头押注(我们称为一轮),没到达连赢目标之前输都算失败,第一次都从 1 元开始(达到目标前输掉都会重新从 1 元开始押注)。只赢一次、两次、三次后输掉的情况如下:
可以看出: 不管设置赢得目标次数是几,每次失败,都是亏损「第一次押注的金额」 继续以 63 元赌金为例,以「反马丁格尔策略」的操作方法来操作,你要输光,就必须让庄家连开 63 次与你押注相反的盘,这种情况一百万兆次才会发生一次 有点懵逼?没关系,我们再通过感性认识去理解一下 想象一下,我们站在一座山丘上,堆了四个雪球(1 元开始押注),我们同一时间将雪球往下推,假设其中三个雪球都在途中被石头啦、树木啦撞坏了(此轮失败),只有一个顺利滚到山下(达成目标连赢),那么它现在已经变得非常的大,可能是当初雪球大小的十倍或百倍大小(获利)[p] 有没有好理解一些? 传统的「马丁格尔」以及「反马丁格尔」策略都是以
总结一下,这个策略有两点比较关键:
分别对应
看到这里是不是有点蠢蠢欲动?笔者也是,所以我用 Python 写了个小程序
定义一个赌局
参数
返回:
import random WIN = 1 LOSE = 0 def gambling_50_percent(pocket, pay): result = random.randint(0, 1) if result == WIN: pocket += pay else: pocket -= pay return result, pocket
注解:赢了会赢押注相同的钱,输了赌注被庄家收走
定义一轮游戏
参数解释:
def play_a_round(win_time_to_stop, pocket, pay, n): money_when_start = pocket root_pay = pay for i in xrange(win_time_to_stop): win_or_lose, pocket = gambling_50_percent(pocket, pay) if win_or_lose == WIN: pay *= n else: pay = root_pay break print pocket, pay return pocket - money_when_start, pocket > money_when_start
注解:此方法是模拟一轮(win_time_to_stop 次)游戏,只有两种结果,即:
循环中,如果输一次,那么直接跳出循环,结束此轮;没输就继续玩直到「目标连赢次数」,最终返回金额变动(pocket - money_when_start)和输赢结果(pocket > money_when_start)
玩几把
兜里:63 元 首次赌注:1 元 押注递增系数:2 倍 目标连赢次数:4 次[p] 根据我们前文的分析,每输一轮,只会亏损「第一次押注的金额」 十个雪球全部滚失败,损失:
[p] 一个雪球滚成功,获利: 九个雪球滚失败,损失: 最终结果: 两个雪球滚成功,获利: 八个雪球滚失败,损失: 最终结果: |
|



 [p]滚雪球~[/p][/p]
[p]滚雪球~[/p][/p]
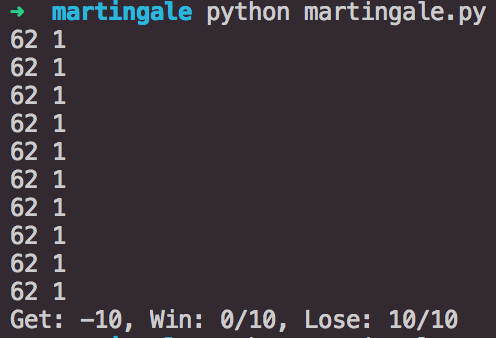 [p]连输 10 轮[/p][/p]
[p]连输 10 轮[/p][/p]
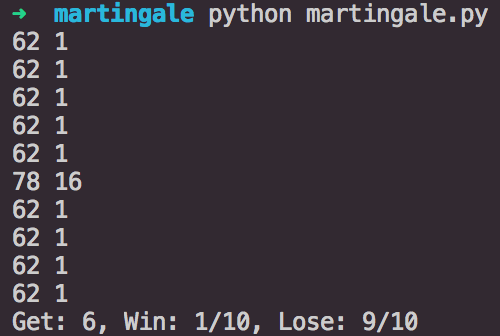 [p]一个雪球滚成功啦[/p][/p]
[p]一个雪球滚成功啦[/p][/p]
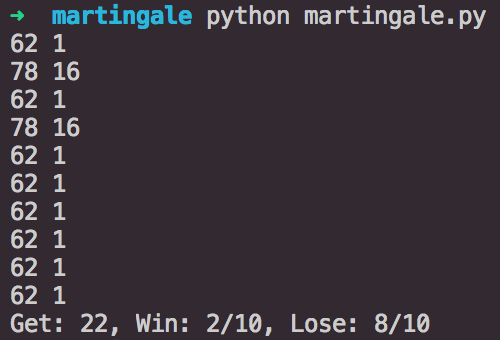 [p]两个雪球,不可思议![/p][/p]
[p]两个雪球,不可思议![/p][/p]
